Bài 1: Xét thiết kế của một hệ thống thông tin liên lạc. Hỏi có bao nhiêu mã vùng
a) Gồm 3 số?
b) Gồm 3 số trong đó số 0 hoặc 1 chỉ xuất hiện ở giữa?
c) Gồm 3 số trong đó không có số nào xuất hiện nhiều hơn một lần?
Bài 2: Một máy chủ sử dụng mật khẩu có đúng 8 kí tự, mỗi kí tự có thể là 1 trong số 26 chữ thường (a-z) hoặc 26 chữ in hoa (A-Z) hoặc 10 số nguyên (0-9). Kí hiệu $\Omega$ là tập hợp tất cả các mật khẩu có thể có, kí hiệu X và Y tương ứng là các sự kiện “mật khẩu chỉ có chữ cái” và “mật khẩu chỉ có số nguyên”. Xác định số lượng mật khẩu trong mỗi sự kiện sau:
a) $\Omega, X$ và $\overline{X}\cap\overline{Y}$.
b) Mật khẩu chứa ít nhất một số nguyên.
c) Mật khẩu chứa đúng một số nguyên.
Bài 3: Một byte được định nghĩa là một chuỗi gồm 8 bit. Mỗi bit có thể nhận giá trị là 0 hoặc 1. Có thể có bao nhiêu byte khác nhau?
Bài 4: Một lô 140 chip được kiểm tra bằng cách chọn một mẫu 5 chip. Giả sử có 10 chip không phù hợp với yêu cầu của khách hàng.
a) Có bao nhiêu mẫu khác nhau?
b) Có bao nhiêu mẫu trong đó chứa chính xác một chip không phù hợp?
c) Có bao nhiêu mẫu trong đó chứa ít nhất một chip không phù hợp?
Bài 5: Trong thiết kế của một sản phẩm cơ điện, 12 thành phần được xếp chồng lên nhau thành một vỏ hình trụ nhằm giảm thiểu tác động của các va chạm. Một đầu của vỏ được chỉ định là đáy và đầu kia là đỉnh.
a) Nếu tất cả các thành phần khác nhau thì có bao nhiêu mẫu thiết kế khác nhau?
b) Nếu bảy thành phần giống hệt nhau, nhưng các thành phần còn lại khác nhau thì có bao nhiêu mẫu thiết kế khác nhau?
c) Nếu ba thành phần là một loại, bốn thành phần thuộc loại khác, các thành phần còn lại khác nhau thì có bao nhiêu mẫu thiết kế khác nhau?
Bài 6: Một thẻ tín dụng gồm 16 chữ số. Nếu nhập ngẫu nhiên thì xác suất để thẻ tín dụng đó hợp lệ là bao nhiêu, biết chỉ có $10^8$ thẻ có giá trị sử dụng?
Bài 7: Một máy chủ sử dụng mật khẩu có đúng 8 kí tự, mỗi kí tự có thể là 1 trong số 26 chữ thường (a-z) hoặc 26 chữ in hoa (A-Z) hoặc 10 số nguyên (0-9). Kí hiệu X và Y tương ứng là các sự kiện “mật khẩu bắt đầu với nguyên âm (a, e, i, o hoặc u)” và “mật khẩu kết thúc bằng một số chẵn”.
a) Tính $P(X), P(Y)$.
b) Tìm $P(X\cap Y)$ và $P(X\cup Y)$.
c) Một hacker chọn ngẫu nhiên một mật khẩu, hỏi xác suất của mật khẩu được chọn là bao nhiêu khi hacker biết mật khẩu của máy chủ nằm trong sự kiện X.
Bài 8: Để kiểm tra một bảng mạch, người ta sử dụng một mẫu kiểm tra ngẫu nhiên là một mảng gồm 10 bit (1 bit nhận giá trị 0 hoặc 1). Giả sử các bit là độc lập. Hỏi:
a) Xác suất để tất cả các bit có giá trị 1 là bao nhiêu?
b) Xác suất có đúng 5 bit có giá trị 0 và 5 bit có giá trị 1?
Bài 9: Mạch điện hoạt động khi có điện đi từ a đến b. Xác suất để mỗi thiết bị hoạt động được cho trên sơ đồ sau
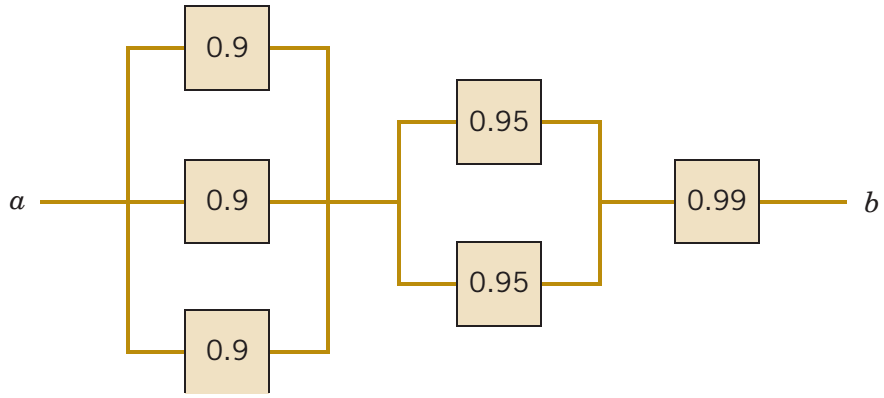
Hỏi xác suất hoạt động của mạch?
Bài 10: Lô hàng 100 chip có 20 chip lỗi
a) Lấy lần lượt 2 chip từ lô hàng, hỏi xác suất chip thứ 2 bị lỗi?
b) Lấy lần lượt 3 chip từ lô hàng, hỏi xác suất để tất cả 3 chip bị lỗi?
Bài 11: Một hệ thống mã hóa-giải mã gồm ba bộ phận: mã hóa, truyền tin và giải mã. Trong quá trình hoạt động, bộ phận mã hóa có xác suất lỗi 0,5%, lỗi ở bộ phận truyền tin là 1% và 0,1% là lỗi của bộ phận giải mã. Giả sử các lỗi là độc lập. Tính xác suất để
a) Một thông báo hoàn toàn không có lỗi nào?
b) Một thông báo bị lỗi hoặc ở bộ phận mã hóa hoặc ở bộ phận giải mã?
Bài 12: Tín hiệu thông tin được phát liên tiếp hai lần. Trạm thu nhận được thông tin trong mỗi lần phát với xác suất bằng 0,35.
a) Tìm xác suất để trạm thu nhận được thông tin đó.
b) Nếu muốn xác suất nhận được thông tin không nhỏ hơn 0,9 thì phải phát tin đó bao nhiêu lần?
Bài 13: Một bộ lọc e-mail được thiết kế để tách các e-mail hợp lệ khỏi e-mail rác. Từ “miễn phí” có trong 60% e-mail rác và trong 4% e-mail hợp lệ. Xác định các xác suất sau biết rằng có đến 20% là e-mail rác:
a) E-mail có chứa từ “miễn phí”.
b) E-mail rác biết nó chứa từ “miễn phí”.
c) E-mail hợp lệ biết nó không chứa từ “miễn phí”.
Bài 14: Tỉ lệ hỏng của chip tùy thuộc vào độ ô nhiễm trong sản xuất. Với độ ô nhiễm cao, trung bình và thấp thì tỉ lệ này tương ứng là 0,1; 0,01 và 0,001. Trong một lô sản xuất có 20% số chip phải chịu mức độ ô nhiễm cao, 30% ở mức độ trung bình và 50% là mức độ thấp. Hỏi xác suất sản xuất 1 con chip không thành công là bao nhiêu?
Bài 15: Một nhóm nghiên cứu về nguy cơ gặp sự cố tại một nhà máy điện nguyên tử sẽ gây ra sự rò rỉ phóng xạ. Nhóm nghiên cứu nhận thấy các loại sự cố chỉ có thể là: hoả hoạn, sự gãy đổ của vật liệu hoặc sai lầm của con người, và 2 hay nhiều hơn 2 sự cố không bao giờ cùng xảy ra. Nếu có hỏa hoạn thì sự rò rỉ phóng xạ xảy ra khoảng 20%. Nếu có sự gãy đổ của vật liệu thì sự rò rỉ phóng xạ xảy ra khoảng 50% và nếu có sự sai lầm của con người thì sự rò rỉ sẽ xảy ra khoảng 10%. Nhóm nghiên cứu cũng tìm được xác suất để: Hoả hoạn và sự rò rỉ phóng xạ cùng xảy ra là 0,0010; gãy đổ vật liệu và sự rò rỉ phóng xạ cùng xảy ra là 0,0015; sai lầm của con người và sự rò rỉ phóng xạ cùng xảy ra là 0,0012. Tìm xác suất để
a) Có hỏa hoạn, có gãy đổ vật liệu và có sai lầm của con người.
b) Có sự rò rỉ phóng xạ.
c) Sự rò rỉ phóng xạ được gây ra bởi sai lầm của con người.



