ĐL152: 11.3. Phương pháp đổi biến trong tích phân bội 3

Công thức đổi biến

Ta cần tìm $\iiint\limits_{V}{f(x,y,z)dxdydz}$.

Thực hiện phép đổi biến: \[\begin{cases}x=x(u,v,w) \\y=y(u,v,w) \\z=z(u,v,w) \\\end{cases} \tag{*}\label{hoa1}\]

Giả sử

1. Các hàm $x(u,v,w);\text{ }y(u,v,w);\text{ }z=z(u,v,w)$ liên tục và có các đạo hàm riêng liên tục trên miền đóng $V'$ nằm trong không gian $Ouvw$.

2. Các công thức \eqref{hoa1} xác định 1 song ánh từ $V'$ lên $V$.

3. Định thức $J=\dfrac{D(x,y,z)}{D(u,v,w)}=\left|\begin{matrix}x{{'}_{u}} & x{{'}_{v}} & x{{'}_{w}} \\y{{'}_{u}} & y{{'}_{v}} & y{{'}_{w}} \\z{{'}_{u}} & z{{'}_{v}} & z{{'}_{w}} \\\end{matrix}\right|\ne 0$, $\forall (u,v,w)\in V'$.

Khi đó ta có công thức đổi biến trong tính tích phân bội 3: \[ \iiint\limits_{V}{f(x,y,z)dxdydz}=\iiint\limits_{V'}{f(x(u,v,w),y(u,v,w),z(u,v,w))|J|dudvdw}\tag{11.5}\label{hoa2}\]

Ví dụ 1. Tính thể tích miền $V$ được giới hạn bởi các mặt sau: $x+y+z=-3,$ $x+y+z=3,$ $x+2y-z=-1,$ $x+2y-z=1,$ $x+4y+z=-2,$ $x+4y+z=2$.

Giải

Thể tích miền $V$ được cho bởi công thức: $V=\iiint\limits_{V}{dxdydz}$.

Thực hiện phép đổi biến $\begin{cases}u=x+y+z \\v=x+2y-z \\w=x+4y+z \\\end{cases}\Rightarrow \begin{cases}x=\dfrac{1}{2}(2u+v-w) \\y=\dfrac{1}{3}(-u+w) \\z=\dfrac{1}{6}(2u-3v+w) \\\end{cases}$

Xác định miền $V'$: $V'=\left\{ (u,v,w)\in {{\mathbb{R}}^{3}}|-3\le u\le 3;-1\le v\le 1;-2\le w\le 2 \right\}$

Dễ thấy phép đổi biến trên xác định một song ánh từ $V'$ lên $V$.

Ta có: \[J=\dfrac{D(x,y,z)}{D(u,v,w)}=\left| \begin{matrix}x{{'}_{u}} & x{{'}_{v}} & x{{'}_{w}} \\y{{'}_{u}} & y{{'}_{v}} & y{{'}_{w}} \\z{{'}_{u}} & z{{'}_{v}} & z{{'}_{w}} \\\end{matrix} \right|=\left| \begin{matrix}1 & \dfrac{1}{2} & -\dfrac{1}{2} \\-\dfrac{1}{3} & 0 & \dfrac{1}{3} \\\dfrac{1}{3} & -\dfrac{1}{2} & \dfrac{1}{6} \\\end{matrix} \right|=\dfrac{1}{6}\ne 0/V'\]

Áp dụng công thức \eqref{hoa2} ta có $V=\iiint\limits_{V}{dxdydz}=\dfrac{1}{6}\int\limits_{-3}^{3}{du}\int\limits_{-1}^{1}{dv}\int\limits_{-2}^{2}{dw}=8$ $(đvtt).$

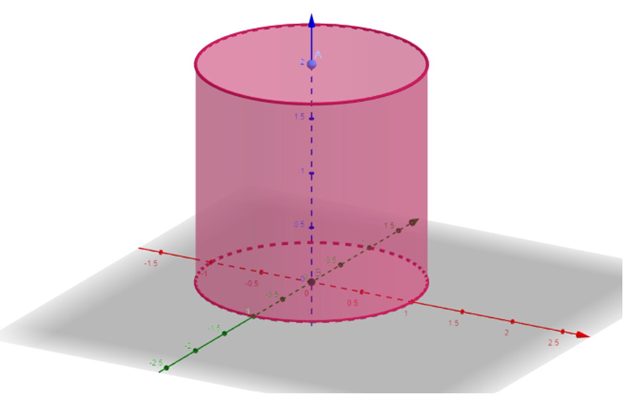
Tính tích phân bội 3 trong hệ tọa độ trụ

Hệ tọa độ trụ

Định nghĩa. Tọa độ trụ của một điểm $M(x,y,z)$ trong không gian $Oxyz$ là 1 bộ có thứ tự gồm 3 số $(r,\varphi ,z)$ trong đó $(r,\varphi )$ là các tọa độ cực của điểm $M'(x,y)$ $(M'$ là hình chiếu vuông góc của $M(x,y,z)$ lên mặt phẳng tọa độ $Oxy).$

Với mọi điểm của không gian ta có: $r\ge 0;\text{ }\varphi \in \text{ }\!\![\!\!\text{ }0,2\pi );\text{ }z\in (-\infty ,+\infty )$.

Công thức tính

Quan hệ giữa các tọa độ Descartes $x,y,z$ và các tọa độ trụ $r,\varphi ,z$ của cùng một điểm $M$: \[\begin{cases}x=r\cos \varphi \\y=r\sin \varphi \\z=z \\\end{cases}\tag{**}\label{hoa3}\]

Nếu $r>0;\text{ }\varphi \in \text{ }\!\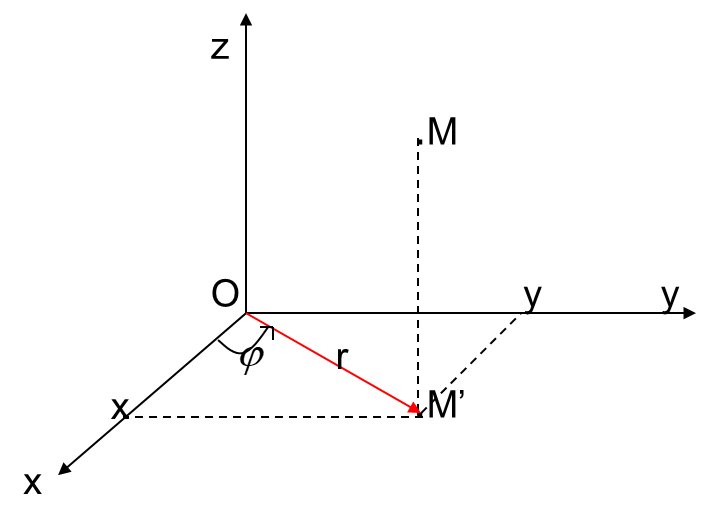![\!\!\text{ }0,2\pi );\text{ }z\in (-\infty ,+\infty )$ thì các công thức \eqref{hoa3} xác định 1 song ánh giữa các tọa độ đề các và tọa độ trụ (riêng các điểm trên trục $Oz$ có $z$ xác định, $r=0$, $\varphi $ tùy ý).

Xem các công thức \eqref{hoa3} như một phép đổi biến, ta có: \[J=\dfrac{D(x,y,z)}{D(r,\varphi ,z)}=\left| \begin{matrix}\cos \varphi & -r\sin \varphi & 0 \\\sin \varphi & r\cos \varphi & 0 \\ 0 & 0 & 1 \\\end{matrix} \right|=r\ne 0\] (trừ tại những điểm trên trục $Oz$)

Ta có công thức tính tích phân bội 3 trong hệ tọa độ trụ như sau: \[\iiint\limits_{V}{f(x,y,z)dxdydz}=\iiint\limits_{V'}{f(r\cos \varphi ,r\sin \varphi ,z)rdrd\varphi dz}\tag{11.6}\label{hoa4}\]

Chú ý

Công thức \eqref{hoa4} vẫn đúng trong trường hợp $V$ chứa những điểm thuộc $Oz$.
Nếu $V$ là hình trụ $0\le r\le R;\text{ }0\le z\le h$ thì: \[\iiint\limits_{V}{f(x,y,z)dxdydz}=\int\limits_{0}^{2\pi }{d\varphi }\int\limits_{0}^{h}{dz}\int\limits_{0}^{R}{f(r\cos \varphi ,r\sin \varphi ,z)rdr}\tag{11.7}\label{hoa5}\]

Ví dụ 2. Tính tích phân $\iiint\limits_{V}{z({{x}^{2}}+{{y}^{2}})dxdydz}$ với $V$ được giới hạn bởi các mặt ${{x}^{2}}+{{y}^{2}}=1;\text{ }z=0;\text{ }z=2$.

Giải

$V$ là hình trụ tròn xoay $0\le r\le 1;\text{ }0\le z\le 2$, nên việc tính toán sẽ đơn giản nếu chuyển sang tọa độ trụ và áp dụng công thức \eqref{hoa5}

Ta có: $$\iiint\limits_{V}{z({{x}^{2}}+{{y}^{2}})dxdydz}=\int\limits_{0}^{2\pi }{d\varphi }\int\limits_{0}^{2}{zdz}\int\limits_{0}^{1}{{{r}^{3}}dr}=\pi $$

Ví dụ 3. Tính tích phân $\iiint\limits_{V}{\sqrt{{{x}^{2}}+{{y}^{2}}}dxdydz}$ với $V$ được giới hạn bởi các mặt ${{x}^{2}}+{{y}^{2}}=2y;\text{ }z=0;\text{ }z=2.$

Giải

Ta có, miền $V$: ${{x}^{2}}+{{(y-1)}^{2}}=1;\text{ }z=0;\text{ }z=2$ là hình trụ tròn xoay, có hình chiếu vuông góc lên mặt phẳng $Oxy$ là miền $D$ - hình tròn tâm $I(0,1)$ bán kính $R=1$, nên việc tính toán sẽ đơn giản nếu chuyển sang tọa độ trụ và áp dụng công thức \eqref{hoa4} với $V'=\left\{ (r,\varphi ,z)|0\le r\le 2\sin \varphi ;\text{ }0\le \varphi \le \pi ;\text{ }0\le z\le 2 \right\}.$

Ta có: $$\iiint\limits_{V}{\sqrt{{{x}^{2}}+{{y}^{2}}}dxdydz}=\iiint\limits_{V'}{{{r}^{2}}drd\varphi dz}=\int\limits_{0}^{\pi }{d\varphi }\int\limits_{0}^{2}{dz}\int\limits_{0}^{2\sin \varphi }{{{r}^{2}}dr}=\dfrac{64}{9}$$

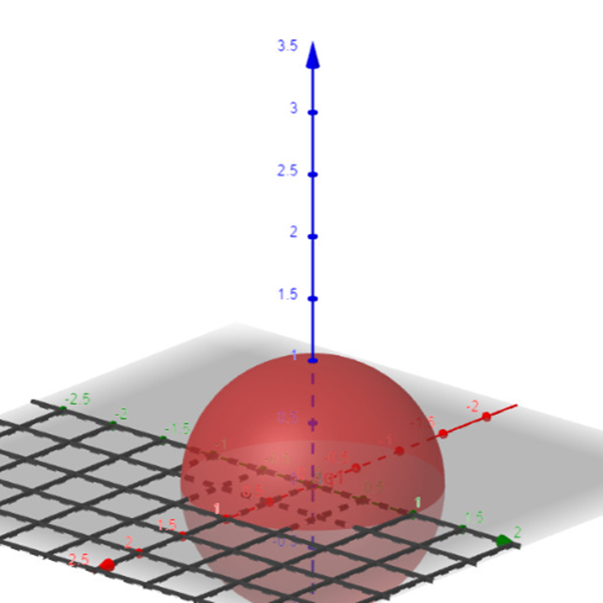
Tính tích phân bội 3 trong hệ tọa độ cầu

Hệ tọa độ cầu

Định nghĩa. Tọa độ cầu của một điểm $M(x,y,z)$ trong không gian $Oxyz$ là một bộ có thứ tự gồm 3 số $(r,\theta ,\varphi )$ với $r=OM,\varphi =\left( Ox,\overrightarrow{OM'} \right),\theta =\left( \overrightarrow{OM},Oz \right);$ $r\ge 0;\text{ }\varphi \in \text{ }\!\![\!\!\text{ }0,2\pi );\text{ }\theta \in \text{ }\!\![\!\!\text{ }0,\pi )$ trong đó điểm $M'(x,y)$ là hình chiếu vuông góc của $M(x,y,z)$ lên mặt phẳng tọa độ $Oxy.$

Công thức tính

Quan hệ giữa các tọa độ Descartes $x,y,z$ và các tọa độ cầu $r,\theta ,\varphi $ của cùng một điểm $M$: \[ \begin{cases}x=r\sin \theta \cos \varphi \\y=r\sin \theta \sin \varphi \\z=r\cos \theta \\\end{cases}\tag{***}\label{hoa6}\]

Nếu $r>0;\text{ }\varphi \in \text{ }\!\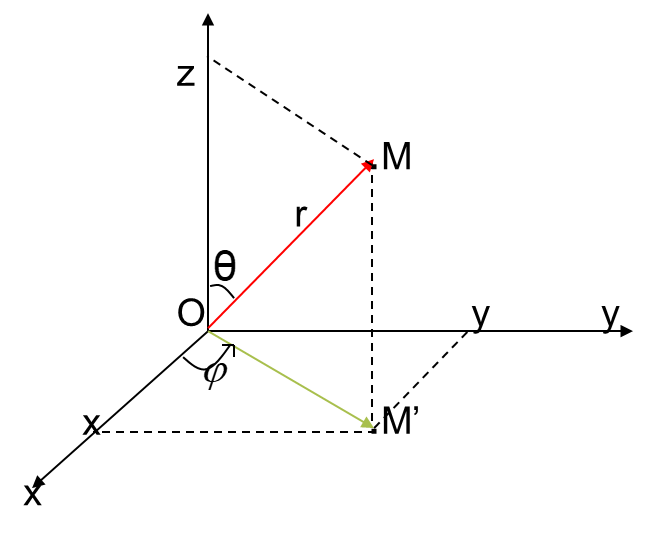![\!\!\text{ }0,2\pi );\text{ }\theta \in (0,\pi )$ thì các công thức \eqref{hoa6} xác định một song ánh giữa các tọa độ đề các và tọa độ cầu (riêng các điểm trên trục $Oz$ có $\theta =0,$ $\varphi $ tùy ý và nếu $M\equiv O$ thì có $r=0;\text{ }\theta =0$, $\varphi $ tùy ý).

Xem các công thức \eqref{hoa6} như một phép đổi biến, ta có: \[|J|=\left| \dfrac{D(x,y,z)}{D(r,\theta ,\varphi )} \right|={{r}^{2}}\sin \theta >0\] (trừ tại những điểm trên trục $Oz$ )

Ta có công thức tính tích phân bội 3 trong hệ tọa độ cầu như sau: \[\iiint\limits_{V}{f(x,y,z)dxdydz}=\iiint\limits_{V'}{f(r\sin \theta \cos \varphi ,r\sin \theta \sin \varphi ,r\cos \theta ){{r}^{2}}\sin \theta drd\theta d\varphi }\tag{11.8}\label{hoa7}\]

Chú ý

Công thức \eqref{hoa4} vẫn đúng trong trường hợp $V$ chứa những điểm thuộc $Oz$.
Nếu $V$ là hình cầu tâm $O(0,0,0)$ bán kính $R$ thì ta có công thức: \[\iiint\limits_{V}{f(x,y,z)dxdydz}=\int\limits_{0}^{2\pi }{d\varphi }\int\limits_{0}^{\pi }{\sin \theta d\theta }\int\limits_{0}^{R}{f(r\sin \theta \cos \varphi ,r\sin \theta \sin \varphi ,r\cos \theta ){{r}^{2}}dr}\tag{11.9}\label{hoa8}\]

Ví dụ 4. Tính tích phân $\iiint\limits_{V}{\sqrt{{{x}^{2}}+{{y}^{2}}+{{z}^{2}}}dxdydz}$ với $V$ được giới hạn bởi các mặt ${{x}^{2}}+{{y}^{2}}+{{z}^{2}}=1;\text{ }z\ge 0$.

Giải

$V$ là nửa hình cầu tâm $O(0,0,0)$ bán kính $R=1$ nằm phía trên mặt phẳng tọa độ $Oxy$ (ứng với $z\ge 0)$, nên việc tính toán sẽ đơn giản nếu chuyển sang tọa độ cầu và áp dụng công thức \eqref{hoa8}

Ta có: $$\iiint\limits_{V}{\sqrt{{{x}^{2}}+{{y}^{2}}+{{z}^{2}}}dxdydz}=\int\limits_{0}^{2\pi }{d\varphi }\int\limits_{0}^{\pi /2}{\sin \theta \text{ }d\theta }\int\limits_{0}^{1}{r{{r}^{2}}dr}=\dfrac{\pi }{2}$$

Ví dụ 5. Tính tích phân $\iiint\limits_{V}{zdxdydz}$ với miền $V$ được giới hạn bởi các mặt $\text{ }z=0;\text{ }z=\sqrt{{{R}^{2}}-{{x}^{2}}-{{y}^{2}}}$.

Giải

Ngoài cách tính như trình bày ở ví dụ 2, mục 11.2 (áp dụng công thức (3)) ta có thể chuyển sang tọa độ cầu và áp dụng công thức \eqref{hoa8}: $$\iiint\limits_{V}{zdxdydz}=\int\limits_{0}^{2\pi }{d\varphi }\int\limits_{0}^{\pi /2}{\sin \theta \cos \theta d\theta }\int\limits_{0}^{R}{r{{r}^{2}}dr}=\dfrac{\pi {{R}^{4}}}{4}$$

{discussion:1161.11.3}

Last modified: Thursday, 5 September 2024, 10:01 AM

11.3. Phương pháp đổi biến trong tích phân bội 3

11.3. Phương pháp đổi biến trong tính tích phân bội 3