11.2. Cách tính tích phân bội 3 trong hệ tọa độ Descartes

Trước hết ta nên vẽ hình biểu diễn miền $V$ để dễ dàng hơn trong biểu diễn miền $V$ trong hệ tọa độ Descartes:

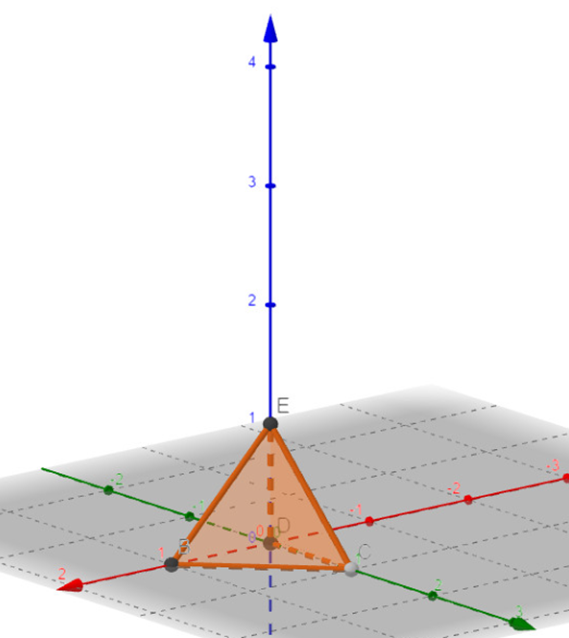$V$ được xác định bởi các bất đẳng thức kép \(\begin{cases}0\le x\le 1 \\0\le y\le 1-x \\0\le z\le 1-x-y \\\end{cases}\)

Sau đó, thay vào công thức (2) \eqref{hoa1} và tính tích phân (lưu ý: phải tính tích phân theo biến $z$ trước, tiếp theo đến tích phân theo biến $y$ và cuối cùng là tích phân theo biến $x$)

$$\iiint\limits_{V}{(1-x-y)dxdydz}=\int\limits_{0}^{1}{dx\int\limits_{0}^{1-x}{dy\int\limits_{0}^{1-x-y}{(1-x-y)dz}}}=\int\limits_{0}^{1}{dx\int\limits_{0}^{1-x}{\left. (1-x-y)z \right|_{0}^{1-x-y}dy}}$$

$$=\int\limits_{0}^{1}{dx\int\limits_{0}^{1-x}{{{(1-x-y)}^{2}}dy}}=-\int\limits_{0}^{1}{dx\int\limits_{0}^{1-x}{{{(1-x-y)}^{2}}d(1-x-y)}}=-\dfrac{1}{3}\int\limits_{0}^{1}{\left. {{(1-x-y)}^{3}} \right|_{0}^{1-x}dx}$          $=\dfrac{1}{3}\int\limits_{0}^{1}{{{(1-x)}^{3}}dx}=-\dfrac{1}{3}\int\limits_{0}^{1}{{{(1-x)}^{3}}d(1-x)}=-\dfrac{1}{12}\left. {{(1-x)}^{4}} \right|_{0}^{1}=\dfrac{1}{12}$$.

Những trường hợp khó vẽ hình biểu diễn miền $V$ thì ta phải cố gắng tưởng tượng để đưa ra được miền $V$, hình chiếu của nó xuống mặt phẳng tọa độ $Oxy$ (miền $D$)

 $V$ là nửa hình cầu tâm $O(0,0,0)$ bán kính $R$ nằm trên mặt phẳng tọa độ $Oxy$ (ứng với $z\ge 0)$ còn $D$ là hình tròn tâm $O(0,0)$ bán kính $R$, do đó ta nên áp dụng công thức \eqref{hoa2} $$\iiint\limits_{V}{zdxdydz}=\iint\limits_{{{x}^{2}}+{{y}^{2}}\le {{R}^{2}}}{dxdy}\int\limits_{0}^{\sqrt{{{R}^{2}}-{{x}^{2}}-{{y}^{2}}}}{zdz}=\dfrac{1}{2}\iint\limits_{{{x}^{2}}+{{y}^{2}}\le {{R}^{2}}}{\left. {{z}^{2}} \right|_{0}^{\sqrt{{{R}^{2}}-{{x}^{2}}-{{y}^{2}}}}dxdy}$$

Chuyển sang tọa độ cực, ta có $$\iiint\limits_{V}{zdxdydz}=\dfrac{1}{2}\int\limits_{0}^{2\pi }{d\varphi }\int\limits_{0}^{R}{({{R}^{2}}-{{r}^{2}})}rdr=\dfrac{\pi {{R}^{4}}}{4}$$.