Thảo luận nội dung "Khái niệm hàm số nhiều biến số
7.1. Khái niệm hàm số nhiều biến số
Completion requirements
7.1. Khái niệm về hàm nhiều biến
Hàm 2 biến
Định nghĩa. Xét tích Đề các
${{\mathbb{R}}^{2}}$ và tập $D\subset {{\mathbb{R}}^{2}}$.
Ánh xạ bất kỳ $f:D\to \mathbb{R}$ là một hàm 2 biến xác định trên $D$.
$D$ được gọi là tập xác định hay miền xác định của hàm $f$.
Như vậy. Một hàm hai biến xác
định trên $D$ là một phép tương ứng: cho ứng mỗi cặp số thực có
thứ tự $(x,y)\in D$ với một số thực xác định mà ta kí hiệu là
$f(x,y)$.
Biểu diễn của hàm $f$ là $f: (x, y)\mapsto z=f(x, y)$ hay $z=f(x,y)$.
Trong đó $x,y$ được gọi là các biến độc lập và $z$ được gọi là biến phụ thuộc, $f(x,y)$ là ảnh của $(x,y)$ qua ánh xạ $f$ (hay trị của $f$ tại $(x,y)$).
Tập $f(D)=\left\{ z\in \mathbb{R}|\exists (x,y)\in D:f(x,y)=z \right\}$ được gọi tập giá trị hay miền giá trị của hàm $f$.
Quy ước: Nếu hàm được xác định bởi
một biểu thức nào đó và không nói gì thêm thì miền xác định là
tập tất cả các cặp số thực có thứ tự mà ứng với nó biểu thức đã
cho có nghĩa.
Ví dụ 1. $z=3{{x}^{2}}y+2022$
là hàm 2 biến xác định trên ${{\mathbb{R}}^{2}}$.
Ví dụ 2.
$z=\dfrac{1}{\sqrt{1-{{x}^{2}}-{{y}^{2}}}}$ là hàm 2 biến xác
định trên $D=\left\{ (x,y)\in
{{\mathbb{R}}^{2}}|{{x}^{2}}+{{y}^{2}}<1 \right\}$.
Ví dụ 3.
$z=\dfrac{x{{e}^{y}}}{{{x}^{2}}+{{y}^{2}}}$ là hàm 2 biến xác
định trên ${{\mathbb{R}}^{2}}\backslash \left\{ (0,0)
\right\}$.
Các khái niệm: tập hợp phẳng, tập hợp mở, tập hợp đóng
Tập hợp phẳng (tập phẳng): là
tập các điểm cùng nằm trong một mặt phẳng.
Một tập phẳng được gọi là tập giới nội (hay tập bị chặn) nếu tồn tại một mặt tròn chứa nó.
Chú ý. Miền xác định của hàm
$z=f(x,y)$ là một tập phẳng nằm trong mặt phẳng $Oxy$.
Ví dụ 4. Miền xác định của
hàm số $z=\sqrt{1-{{x}^{2}}-{{y}^{2}}}$ là tập phẳng giới nội
$D=\left\{ (x,y)\in {{\mathbb{R}}^{2}}|{{x}^{2}}+{{y}^{2}}\le 1
\right\}$ (hình tròn tâm $O(0,0)$ bán kính $r=1$) nằm trong mặt
phẳng $Oxy$.
Tập hợp mở, tập hợp đóng
Ta gọi $\delta -$lân cận của điểm ${{M}_{0}}({{x}_{0}},{{y}_{0}})$ trong mặt phẳng là tập tất cả những điểm $M(x,y)$ của mặt phẳng sao cho khoảng cách ${{M}_{0}}M<\delta $ (là phần trong của mặt tròn tâm ${{M}_{0}}({{x}_{0}},{{y}_{0}})$ bán kính $\delta $).
Lân cận của ${{M}_{0}}({{x}_{0}},{{y}_{0}})$ là mọi tập hợp chứa một $\delta -$lân cận của điểm ${{M}_{0}}({{x}_{0}},{{y}_{0}})$.
Xét tập $E\subset {{\mathbb{R}}^{2}}$
Điểm $M$ của $E$ được gọi là điểm trong của $E$ nếu tồn tại một lân cận nào đó của nó nằm hoàn toàn trong $E$.
Tập $E$ được gọi là tập mở (hở) nếu mọi điểm của nó đều là điểm trong.
Điểm $N$ được gọi là điểm biên của $E$ nếu mọi lân cận của nó vừa chứa những điểm thuộc $E$ vừa chứa những điểm không thuộc $E$ (điểm biên của một tập hợp có thể thuộc tập hợp ấy cũng có thể không thuộc tập hợp ấy)
Tập tất cả những điểm biên của $E$ được gọi là biên của $E$.
Tập $E$ được gọi là tập đóng (kín) nếu nó chứa mọi điểm biên của nó (nghĩa là: biên của $E$ là một bộ phận của $E$).
Ví dụ 5.
Miền xác định của hàm số $z=\sqrt{1-{{x}^{2}}-{{y}^{2}}}$ là tập đóng.
Miền xác định của hàm số $z=\dfrac{1}{\sqrt{1-{{x}^{2}}-{{y}^{2}}}}$ là tập mở.
Hàm điểm – biểu diễn hình học của hàm 2 biến
Khái niệm. Xét hàm số hai biến
$f: (x, y)\mapsto z=f(x, y)$.
Mỗi cặp số thực $(x,y)$ đều được biểu diễn bởi một điểm $M(x,y)$ trong mặt phẳng $Oxy$, nên ta có thể xem hàm 2 biến $f(x,y)$ là hàm của điểm $M(x,y)$, nghĩa là $f:M\mapsto f(M)$.
Ta biểu diễn hình học một hàm 2 biến như sau:
|
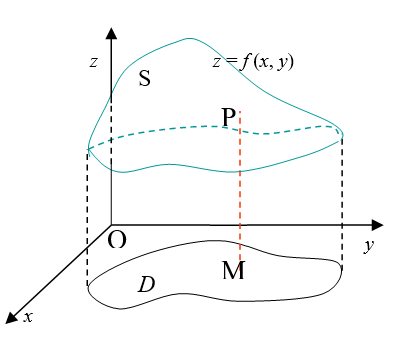
Vẽ hệ trục tọa độ đề các $Oxyz$. Với mỗi điểm $M(x,y)$ trong mặt phẳng $Oxy$ cho ứng với một điểm $P(x,y,z)$ trong không gian với $z=f(x,y)$. Tập các điểm $P(x,y,z)$ khi $M(x,y)$ chạy trong $D$ được gọi là đồ thị của hàm số $z=f(x,y)$ xác định trên $D$ (thường là một mặt cong trong không gian 3 chiều). |
 |
Ví dụ 6.
| Đồ thị hàm số $z=\sqrt{1-{{x}^{2}}-{{y}^{2}}}$ là nửa mặt cầu tâm $O(0,0,0)$, bán kính $r=1$ nằm về phía $z\ge 0$. |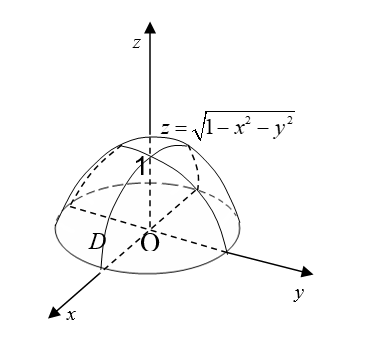
 |
Hàm $n$ biến ($n\ge 3$)
Định nghĩa. Xét $D\subset
{{\mathbb{R}}^{n}}$
Ánh xạ bất kỳ $f:D\to \mathbb{R}$ là một hàm $n$ biến xác định trên $D$.
Viết $f: ({{x}_{1}},{{x}_{2}},...{{x}_{n}})\mapsto u=f({{x}_{1}},{{x}_{2}},...{{x}_{n}})$ hay $u=f({{x}_{1}},{{x}_{2}},...{{x}_{n}})$.
Ví dụ 7. $u={{e}^{xyz}}$ là
hàm 3 biến xác định trên ${{\mathbb{R}}^{3}}$.
Ví dụ 8.
$u=\sqrt{1-{{x}^{2}}-{{y}^{2}}-{{z}^{2}}}$ là hàm 3 biến xác
định trên hình cầu tâm $O(0,0,0)$, bán kính $r=1$.
Chú ý
1. Hàm $n$ biến cũng được xem là hàm điểm.
2. Các định nghĩa về lân cận, tập đóng, tập mở tương tự các định nghĩa tương ứng của hàm 2 biến.
3. Các định nghĩa về tổng, hiệu, tích, thương của 2 hàm, phép hợp các hàm $n$ biến ($n\ge 2$) cũng tương tự các định nghĩa tương ứng của hàm 1 biến.
Tập liên thông
Định
nghĩa. Tập $E\subset {{\mathbb{R}}^{n}}$
được gọi là tập liên thông nếu có thể nối 2 điểm bất kỳ $M,N$
của nó bởi 1 đường liên tục nằm hoàn toàn trong $E$.
Tập liên thông được gọi là tập đơn liên nếu nó bị giới hạn bởi 1 mặt kín.
Tập liên thông được gọi là tập đa liên nếu nó bị giới hạn bởi nhiều mặt kín rời nhau từng đôi một.
Ví dụ 9. Miền xác định của
hàm số $z=\sqrt{1-{{x}^{2}}-{{y}^{2}}}$ là tập đơn liên.
Last modified: Thursday, 5 September 2024, 9:57 AM