Định nghĩa 5.1: Cho \(D\) là tập
con của \(\mathbb{R}\). Ta gọi dãy hàm trên \(D\) là một họ đếm
được các hàm \({(f_{n})}_n\) xác định trên \(D\).
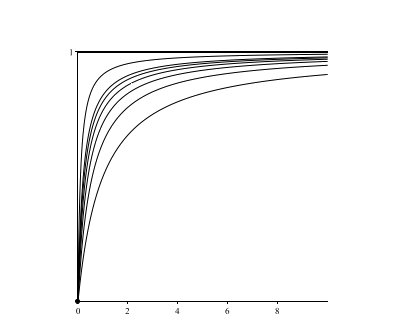
Dãy hàm này được gọi là hội tụ
điểm đến một hàm \(f\) trên \(D\) nếu
\(f(x)=\underset{n\to \infty }{\lim }f_n(x),\) với mọi \( x\in
D.\)
Lúc đó, ta viết \(f=\underset{n\to \infty }{\lim }f_n\) hay
\(f_n\overset{D}{\to }f\). Như vậy
\[f_n\xrightarrow{D}f\Leftrightarrow \forall x\in D,\forall
\epsilon >0,\exists {{n}_{0}}\left( \epsilon ,x
\right),\forall n\ge {{n}_{0}}:\left| {{f}_{n}}(x)-f(x)
\right|<\epsilon.\]
Ví dụ 1: Dãy hàm
\(f_n(x):=\dfrac{nx}{nx+1}\) hội tụ điểm trên tập \(\left[
0;+\infty \right)\) đến hàm \[f(x)=\begin{cases}
0,&\text{nếu }x=0; \\ 1,&\text{nếu }x>0.
\end{cases}\]
Minh họa Ví dụ 1
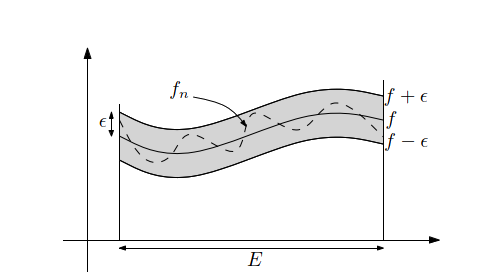
Dãy hàm \((f_n)_n\) được gọi là hội tụ đều trên \(D\) đến hàm \(f\) và
được kí hiệu \(f_n\overset{D}{\rightrightarrows}f\) nếu
\[\forall \epsilon >0,\exists n_0(\epsilon ),\forall n\ge
n_0,\forall x\in D:\left| f_n(x)-f(x) \right|<\epsilon.\]
Dãy hàm \( (f_n)_n\) hội tụ đều đến
\(f\) trên \(D\)
Giả sử \(f_n\) là một dãy hàm xác định trên tập
\(D\subset\mathbb{R}.\) Tương tự định nghĩa tổng của chuỗi số,
với mỗi \(n\in\mathbb{N}\) ta lập hàm tổng riêng
\[S_n(x):=\sum\limits_{k=1}^n f_k(x).\]
Như vậy ta được một dãy hàm mới xác định trên $D$. Nếu dãy hàm
\((S_n)_n\) hội tụ đến một hàm \(S\) thì \(S\) được gọi là tổng
của chuỗi hàm \(\sum\limits_{n=1}^\infty f_n(x)\) trên \(D\) và
ta viết \[S(x)=\sum\limits_{n=1}^{\infty} f_n(x).\]
Nếu dãy \((S_n)_n\) hội tụ đều đến \(S\) ta nói chuỗi hàm
\(\sum\limits_{n=1}^\infty f_n(x)\) hội tụ đều và nếu chuỗi
\(\sum\limits_{n=1}^\infty |u_n(x)|\) hội tụ ta nói chuỗi hàm
hội tụ tuyệt đối. Rõ ràng một chuỗi hàm hội tụ tuyệt đối thì
hội tụ.
Tiêu chuẩn hội tụ đều
Tiêu chuẩn Cauchy
Chuỗi hàm số \(\sum\limits_{n=1}^\infty f_n(x)\) hội tụ đều
trên \(D\) khi và chỉ khi với mọi \(\epsilon>0\) tồn tại một
số \(N\in\mathbb{R}\) sao cho với mọi \(p>q>N\) ta có \[|
S_p(x)-S_q(x)| <\epsilon, \forall x\in D.\]
b. Tiêu chuẩn Weierstrass
Cho chuỗi hàm số \(\sum\limits_{n=1}^\infty f_n(x)\). Nếu tồn
tại chuỗi số dương \(\sum\limits_{n=1}^\infty a_n\) hội tụ và
với mọi \(x\in D\) thỏa mãn \(| f_n(x)|\leq a_n\) (\(\forall
n\in\mathbb{N}\)), khi đó chuỗi hàm \(\sum\limits_{n=1}^\infty
f_n(x)\) hội tụ tuyệt đối và đều trên \(D\).
