10.2. Cách tính tích phân bội 2 trong hệ tọa độ Descartes

Việc tính tích phân bội 2 trực tiếp từ định nghĩa rất phức tạp. Ở đây ta đưa ra cách tính tích phân bội 2 bằng cách dựa vào ý nghĩa hình học của nó.

Miền lấy tích phân là hình chữ nhật có các cạnh song song với các trục tọa độ

Miền $D$ được xác định bởi: \(\begin{cases}a\le x\le b \\c\le y\le d \\\end{cases}\). Giả sử $f(x,y)$ liên tục, không âm trên $D$. Ta có:  $V=\iint\limits_{D}{f(x,y)dxdy}$ ($V$ là vật thể hình trụ có đáy là miền $D$ nằm trong mặt phẳng $Oxy$, xung quanh là mặt trụ có đường sinh song song với trục $Oz$ và phía trên là một mặt cong có phương trình $z=f(x,y)$) Gọi $S(x)$ là diện tích thiết diện vuông góc với $Ox$ tại $x\in \text{ }\!\![\!\!\text{ }a,b\text{ }\!\!]\!\!\text{ }$ của vật thể.

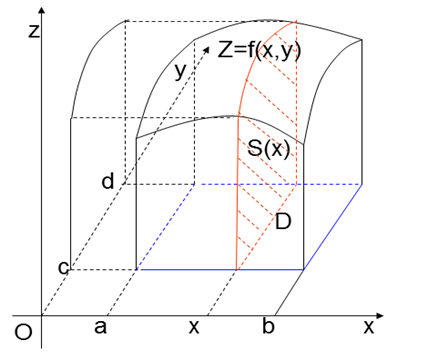Theo ứng dụng của tích phân xác định thì thể tích của vật thể hình trụ được cho bởi công thức  $V=\int\limits_{a}^{b}{S(x)dx}$

Vì $f(x,y)$ liên tục trên $D$ nên $S(x)$ liên tục trên $\text{ }\!\![\!\!\text{ }a,b\text{ }\!\!]\!\!\text{ }$, do đó $S(x)$ khả tích trên $\text{ }\!\![\!\!\text{ }a,b\text{ }\!\!]\!\!\text{ }$.

Mặt khác $S(x)$ là diện tích hình thang cong có đáy là $[c,d]$, cạnh cong có phương trình $z=f(x,y)$ (trong đó $x$ được xem là hằng số)

Theo ứng dụng của tích phân xác định thì $S(x)=\int\limits_{c}^{d}{f(x,y)dy}$.

Vậy, ta có:  $V=\iint\limits_{D}{f(x,y)dxdy}=\int\limits_{a}^{b}{\left[ \int\limits_{c}^{d}{f(x,y)dy} \right]dx}$

Cũng có thể viết: \[\iint\limits_{D}{f(x,y)dxdy}=\int\limits_{a}^{b}{dx}\int\limits_{c}^{d}{f(x,y)dy}\tag{10.2}\label{hoa1}\]

1. Công thức \eqref{hoa1} vẫn đúng khi $f(x,y)$ liên tục và âm trên $D$.
2. Việc tính tích phân bội 2 được đưa về tính hai tích phân đơn liên tiếp.

   Lưu ý. Khi tính tích phân bội 2 ở công thức \eqref{hoa1} ta phải tính $\int\limits_{c}^{d}{f(x,y)dy}$ trước  (ta xem $x$ là hằng số).

3. Thay vì tính thể tích của vật thể hình trụ bởi công thức $V=\int\limits_{a}^{b}{S(x)dx}$ ta có thể  tính bởi công thức $V=\int\limits_{c}^{d}{S( y)dy}$ (trong đó $S( y)$ là diện tích thiết diện vuông góc với $Oy$ tại $y\in [c,d]$ của vật thể đã cho), ta cũng có  $S( y)=\int\limits_{a}^{b}{f(x, y)dx}$.

   Do đó,   $\iint\limits_{D}{f(x,y)dxdy}=\int\limits_{c}^{d}{dy}\int\limits_{a}^{b}{f(x,y)dx}$

   Như vậy, \[\int\limits_{a}^{b}{dx}\int\limits_{c}^{d}{f(x,y)dy}=\int\limits_{c}^{d}{dy}\int\limits_{a}^{b}{f(x,y)dx} \tag{10.3}\label{hoa2}\] \eqref{hoa2}  được gọi là công thức đổi thứ tự lấy tích phân bội 2.

4. Nếu $f(x, y)={{f}_{1}}(x).{{f}_{2}}( y)$ thì:  \[\iint\limits_{D}{f(x, y)dxdy}=\int\limits_{a}^{b}{{{f}_{1}}(x)dx}\int\limits_{c}^{d}{{{f}_{2}}( y)dy}\tag{10.4}\label{hoa3}\]

   Trong trường hợp này tích phân bội 2 bằng tích của 2 tích phân đơn nên ta tính các tích phân đơn độc lập (tích phân nào trước cũng được) rồi đem kết quả nhân với nhau.

Miền lấy tích phân bất kỳ

Trường hợp 1. Miền $D$ được xác định bởi: \(\begin{cases}a\le x\le b \\{{y}_{1}}(x)\le y\le {{y}_{2}}(x) \\\end{cases}\) 

(với ${{y}_{1}}(x), {{y}_{2}}(x)$ là những hàm liên tục và đơn trị trên $[a,b])$.

Giả sử $f(x,y)$ liên tục, không âm trên $D$.

Tương tự như trường hợp $D$ là hình chữ nhật có các cạnh song song với các trục tọa độ, ta có:  $V=\iint\limits_{D}{f(x,y)dxdy}=\int\limits_{a}^{b}{S(x)dx}$ với $S(x)$ là diện tích thiết diện vuông góc với $Ox$ tại $x\in \text{ }\!\![\!\!\text{ }a,b\text{ }\!\!]\!\!\text{ }$ của vật thể.

Mặt khác, $S(x)$ là diện tích hình thang cong có đáy là $[{{y}_{1}}(x),{{y}_{2}}(x)\text{ }\!\!]\!\!\text{ }$, cạnh cong có phương trình $z=f(x,y)$.

Nghĩa là: $S(x)=\int\limits_{{{y}_{1}}(x)}^{{{y}_{2}}(x)}{f(x,y)dy}$

Do đó, $\iint\limits_{D}{f(x,y)dxdy}=\int\limits_{a}^{b}{\left[ \int\limits_{{{y}_{1}}(x)}^{{{y}_{2}}(x)}{f(x,y)dy} \right]dx}$

Cũng có thể viết: \[\iint\limits_{D}{f(x,y)dxdy}=\int\limits_{a}^{b}{dx}\int\limits_{{{y}_{1}}(x)}^{{{y}_{2}}(x)}{f(x,y)dy}\tag{10.5}\label{hoa4}\]

Trường hợp 2. Miền $D$ được xác định bởi:  \(\begin{cases}{{x}_{1}}( y)\le x\le {{x}_{2}}( y) \\c\le y\le d \\\end{cases}\)

(với ${{x}_{1}}( y),{{x}_{2}}( y)$ là những hàm liên tục và đơn trị trên $[c,d])$

Giả sử $f(x, y)$ liên tục, không âm trên $D$.

Tương tự như trường hợp 1, ta có:  $V=\iint\limits_{D}{f(x, y)dxdy}=\int\limits_{c}^{d}{S( y)dy}$

Với $S( y)$ là diện tích thiết diện vuông góc với $Oy$ tại $y\in [c,d]$ của vật thể.

$S( y)$ là diện tích hình thang cong có đáy là $[{{x}_{1}}( y),{{x}_{2}}( y)\text{ }\!\!]\!\!\text{ }$, cạnh cong có phương trình $z=f(x, y)$.

Nghĩa là:  $S( y)=\int\limits_{{{x}_{1}}( y)}^{{{x}_{2}}( y)}{f(x, y)dx}$

Do đó, $\iint\limits_{D}{f(x, y)dxdy}=\int\limits_{c}^{d}{\left[ \int\limits_{{{x}_{1}}( y)}^{{{x}_{2}}( y)}{f(x, y)dx} \right]dy}$

Cũng có thể viết: \[\iint\limits_{D}{f(x,y)dxdy}=\int\limits_{c}^{d}{dy}\int\limits_{{{x}_{1}}( y)}^{{{x}_{2}}( y)}{f(x, y)dx}\tag{10.6}\label{hoa5}\]

Trường hợp. $D$ là miền bất kì (miền lồi- mọi đường thẳng song song với các trục $Ox, Oy$ cắt $D$ tại tối đa 2 điểm) thì ta sẽ đưa về 1 trong 2 trường hợp trên đây.

Và $f(x,y)$ liên tục, đơn trị và không âm trên $D$.

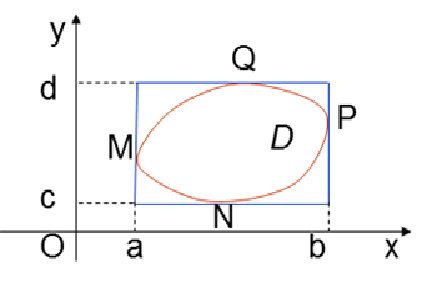
Dựng hình chữ nhật nhỏ nhất chứa $D$ (có các cạnh song song với $Ox,Oy)$. Giả sử, hình chữ nhật ấy được xác định bởi: \(\begin{cases}a\le x\le b \\c\le y\le d \\\end{cases}\) Gọi M, N, P, Q là các giao điểm của biên hình chữ nhật với biên của $D$. Các điểm M và P chia biên của  thành hai cung: cung MNP và cung MQP có phương trình lần lượt là $y={{y}_{1}}(x);\text{ }y={{y}_{2}}(x)$. Theo trường hợp 1, ta có: $$\iint\limits_{D}{f(x,y)dxdy}=\int\limits_{a}^{b}{dx}\int\limits_{{{y}_{1}}(x)}^{{{y}_{2}}(x)}{f(x,y)dy}$$ Các điểm N và Q chia biên của $D$ thành hai cung: cung NMQ và cung NPQ có phương trình lần lượt là  $x={{x}_{1}}( y);\text{ }x={{x}_{2}}( y)$. Theo trường hợp 2, ta có: $$\iint\limits_{D}{f(x, y)dxdy}=\int\limits_{c}^{d}{dy}\int\limits_{{{x}_{1}}( y)}^{{{x}_{2}}( y)}{f(x, y)dx}$$

Vậy, ta có công thức đổi thứ tự lấy tích phân trong tính tích phân bội 2 (công thức Fubini) như sau: $$\int\limits_{a}^{b}{dx}\int\limits_{{{y}_{1}}(x)}^{{{y}_{2}}(x)}{f(x,y)dy}=\int\limits_{c}^{d}{dy}\int\limits_{{{x}_{1}}( y)}^{{{x}_{2}}( y)}{f(x,y)dx}$$