10.1. Khái niệm tích phân bội 2

Bài toán dẫn đến khái niệm

Tìm thể tích của vật thể hình trụ giới hạn bởi mặt phẳng $Oxy$, một mặt trụ có đường sinh song song với trục $Oz$ và một mặt cong có phương trình $z=f(x,y)$ $(f(x,y)\ge 0)$.

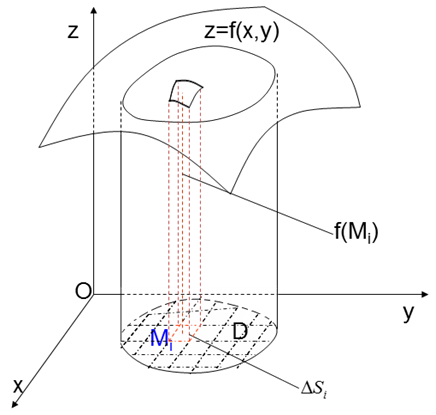Gọi $D$ là miền đóng hữu hạn trong mặt phẳng $Oxy$ giới hạn bởi giao tuyến của mặt trụ và mặt phẳng $Oxy$, $D$ được gọi là đáy của vật thể hình trụ. ($f(x,y)$ liên tục và đơn trị trên $D$)

Chia miền $D$ một cách tùy ý thành $n$ mảnh nhỏ không giẫm lên nhau, gọi tên và cả diện tích của các mảnh ấy là $\Delta {{S}_{1}},\Delta {{S}_{2}},...,\Delta {{S}_{i}},...\Delta {{S}_{n}}$.

Lấy mỗi mảnh nhỏ $\Delta {{S}_{i}}\text{ }(i=\overline{1,n})$ làm đáy, dựng vật thể hình trụ mà mặt xung quanh có đường sinh song song với trục $Oz$, phía trên được giới hạn bởi mặt cong có phương trình $z=f(x,y)$.

Như vậy vật thể hình trụ đang xét được chia thành vật thể hình trụ nhỏ.

Trong mảnh nhỏ $\Delta {{S}_{i}}$ ta lấy một điểm ${{M}_{i}}({{x}_{i}},{{y}_{i}})$ tùy ý , ta có $z({{M}_{i}})=f({{x}_{i}},{{y}_{i}})$. Nếu $\Delta {{S}_{i}}$ khá nhỏ, ta có thể xem thể tích của vật thể hình trụ thứ $i$ là $\Delta {{V}_{i}}$ xấp xỉ thể tích của một hình trụ thẳng có diện tích đáy $\Delta {{S}_{i}}$ và chiều cao chiều cao $z({{M}_{i}})=f({{x}_{i}},{{y}_{i}})$, nghĩa là $\Delta {{V}_{i}}\approx f({{x}_{i}},{{y}_{i}}).\Delta {{S}_{i}}$. Nếu mọi $\Delta {{S}_{i}}$ đều khá nhỏ thì thể tích của vật thể hình trụ là: $V=\sum\limits_{i=1}^{n}{\Delta {{V}_{i}}}\approx \sum\limits_{i=1}^{n}{f({{x}_{i}},{{y}_{i}}).\Delta {{S}_{i}}}$. Phép tính này càng chính xác nếu $n$ càng lớn (các $\Delta {{S}_{i}}$ càng nhỏ, nghĩa là đường kính ${{d}_{i}}$ của $\Delta {{S}_{i}}$ càng nhỏ).

Do đó thể tích của vật thể hình trụ bằng giới hạn nếu có của $\sum\limits_{i=1}^{n}{f({{x}_{i}},{{y}_{i}}).\Delta {{S}_{i}}}$ khi $n\to \infty $ sao cho đường kính lớn nhất trong các đường kính của các $\Delta {{S}_{i}}$ dần tới 0. Nghĩa là: $V=\underset{\max {{d}_{i}}\to 0}{\mathop{\lim\limits }}\,\sum\limits_{i=1}^{n}{f({{x}_{i}},{{y}_{i}})}.\Delta {{S}_{i}}$.

Ngoài bài toán trên, trong các lĩnh vực khác nhau của khoa học kĩ thuật còn có nhiều bài toán mà kết quả đều đưa đến tìm giới hạn của một tổng có dạng trên. Toán học đã định nghĩa cho khái niệm này là tích phân bội 2 hay tích phân kép hay tích phân 2 lớp..

1. Nếu tồn tại tích phân \eqref{hoa1} ta nói $f(x,y)$ khả tích trên $D$.

   Điều kiện khả tích của hàm $f(x,y)$ trên $D$ là $f(x,y)$ liên tục trên $D$.

2. Ý nghĩa hình học: Nếu $f(x,y)\ge 0$ và liên tục trên $D$ thì thể tích của vật thể hình trụ giới hạn bởi mặt phẳng $Oxy$, một mặt trụ có đường sinh song song với trục $Oz$ và một mặt cong có phương trình $z=f(x,y)$ là $V=\iint\limits_{D}{f(x,y)dS}$.

   Đặc biệt, nếu $f(x,y)=1\text{  }\forall (x,y)\in D$ thì $\iint\limits_{D}{dS}={{S}_{D}}$.

3. Giá trị của tích phân bội hai không phụ thuộc vào cách chia miền $D$ nên ta có thể chia $D$ một cách đặc biệt: Chia bởi lưới các đường thẳng song song với các trục $Ox,Oy$. Với cách chia này thì mỗi mảnh $\Delta {{S}_{i}}$ nói chung là một hình chữ nhật, do đó $dS=dxdy$ (vì $x,y$ là các biến độc lập). Vậy, $\iint\limits_{D}{f(x,y)dS}=\iint\limits_{D}{f(x,y)dxdy}$.
4. Tích phân bội hai chỉ phụ thuộc hàm dưới dấu tích phân và miền lấy tích phân chứ không phụ thuộc vào biến tích phân, nghĩa là: $\iint\limits_{D}{f(x,y)dxdy}=\iint\limits_{D}{f(u,v)dudv}$

Tích phân bội 2 có những tính chất tương tự như tính chất của tích phân xác định (tích phân đơn).

1. $\iint\limits_{D}{[f(x,y)\pm g(x,y)]dxdy}=\iint\limits_{D}{f(x,y)dxdy}\pm \iint\limits_{D}{g(x,y)dxdy}$.
2. $\iint\limits_{D}{cf(x,y)dxdy}=c\iint\limits_{D}{f(x,y)dxdy}\text{  }(c-const)$.
3. $D={{D}_{1}}\cup {{D}_{2}}$:  $\iint\limits_{D}{f(x,y)dxdy}=\iint\limits_{{{D}_{1}}}{f(x,y)dxdy}+\iint\limits_{{{D}_{2}}}{f(x,y)dxdy}$.
4. ${{S}_{D}}=\iint\limits_{D}{dxdy}$.
5. Nếu $f(x,y)\le g(x,y)\text{  }\forall (x,y)\in D$ thì $\iint\limits_{D}{f(x,y)dxdy}\le \iint\limits_{D}{g(x,y)dxdy}$

   Đặc biệt, Nếu $f(x,y)\ge 0$ thì $\iint\limits_{D}{f(x,y)dxdy}\ge 0$.

6. Nếu $m$  là giá trị nhỏ nhất, $M$  là giá trị lớn nhất của $f(x,y)$ trên $D$ thì: $$m{{S}_{D}}\le \iint\limits_{D}{f(x,y)dxdy}\le M{{S}_{D}}$$
7. Định lý về giá trị trung bình: Nếu $f(x,y)$ liên tục trên miền liên thông $D$ thì trên $D$ tồn tại ít nhất một điểm ${{M}_{0}}({{x}_{0}},{{y}_{0}})$ sao cho: $f({{x}_{0}},{{y}_{0}})=\dfrac{\iint\limits_{D}{f(x,y)dxdy}}{{{S}_{D}}}$.